The first two articles in this series, “Regular Expression Matching Can Be Simple And Fast” and “Regular Expression Matching: the Virtual Machine Approach,” introduced the foundation of DFA-based and NFA-based regular expression matching. Both were based on toy implementations optimized for teaching the basic ideas. This article is based on a production implementation.
I spent the summer of 2006 building Code Search, which lets programmers search for source code using regular expressions. That is, it lets you grep through the world's public source code. We originally planned to use PCRE for the regular expression search, until we realized that it used a backtracking algorithm, meaning it is easy to make searches take exponential time or arbitrary stack depth. Since Code Search accepts regular expressions from anyone on the Internet, using PCRE would have left it open to easy denial of service attacks. As an alternative to PCRE, I wrote a new, carefully reviewed regular expression parser wrapped around Ken Thompson's open source grep implementation, which uses a fast DFA.
Over the next three years, I implemented a handful of new back ends that collectively replaced the grep code and expanded the functionality beyond what is needed for a POSIX grep. The result, RE2, provides most of the functionality of PCRE using a C++ interface very close to PCRE's, but it guarantees linear time execution and a fixed stack footprint. RE2 is now in widespread use at Google, both in Code Search and in internal systems like Sawzall and Bigtable.
As of March 2010, RE2 is an open source project, with all development conducted in public. This article is a tour through the RE2 source code, showing how the techniques in the first two articles apply in a production implementation.
In the early days, regular expressions had a
very simple syntax, mimicking the simple concepts explained in the first article: concatenation,
repetition, and alternation.
There were few bells and whistles: character classes, the + and ? operators,
and the positional assertions ^ and $.
Today, programmers expect a cacophony of bells and whistles.
The job of a modern regular expression parser is to make sense of the din
and distill it back into the original fundamental concepts.
RE2's parser creates a Regexp data structure, defined in
regexp.h.
It is very close to the original egrep syntax, with a few more special cases:
kRegexpLiteralString nodes, which take up less
memory than a concatenation of individual kRegexpLiteral nodes.
kRegexpRepeat nodes even though
that representation cannot be implemented directly;
we'll see how they get compiled out later.
(?i)abc turns into abc with the case-insensitive
bit instead of [Aa][Bb][Cc]. RE2 originally used the latter,
but it was too memory-intensive, especially with the tree-based character classes.
RE2's parser is in parse.cc.
It's a hand-written parser, both to avoid depending on a particular parser generator
and because modern regular expression syntax is irregular enough to warrant special care.
The parser does not use recursive descent, because the recursion depth would be
potentially unbounded and might overflow the stack,
especially in threaded environments.
Instead the parser maintains an explicit parse stack, as a generated LR(1) parser would.
One thing that surprised me is the variety of ways that
real users write the same regular expression.
For example, it is common to see singleton character classes used
instead of escaping—[.] instead of \.—or alternations
instead of character classes—a|b|c|d instead of [a-d].
The parser takes special care to use the most efficient form for these,
so that [.] is still a single literal character and a|b|c|d
is still a character class.
It applies these simplifications during parsing, rather than in a second pass,
to avoid a larger-than-necessary intermediate memory footprint.
RegexpHaving parsed the regular expression, it is now time to process it.
The parsed form is a standard tree, which suggests processing it with
standard recursive traversals. Unfortunately, we cannot assume that there
is enough stack to do that. Some devious user might present us with
a regular expression like ((((((((((a*)*)*)*)*)*)*)*)*)*)*
(but bigger) and cause a stack overflow.
Instead, the traversal of the regular expression must use an
explicit stack. The Walker template hides the stack management, making this restriction
a little more palatable.
In retrospect, I think the tree form and the Walker
might have been a mistake. If recursion is not allowed (as is the case here),
it might work better to avoid the recursive representation entirely,
instead storing the parsed regular expression in reverse Polish notation
as in Thompson's 1968 paper and this example code.
If the RPN form recorded the maximum stack depth used in the expression,
a traversal would allocate a stack of exactly that size and
then zip through the representation in a single linear scan.
The next processing step is simplification,
which rewrites complex operators into simpler ones
to make later processing easier.
Over time, most of the code in RE2's simplification pass moved into the parser,
because simplifying eagerly keeps the intermediate memory footprint down.
Today there is only one task left for the simplifier:
the expansion of counted repetitions like x{2,5} into
a sequence of basic operations like xx(x(x(x)?)?)?.
Once the regular expression uses only the basic operations described in the first article, it can be compiled using the techniques outlined there. It should be easy to see the correspondence.
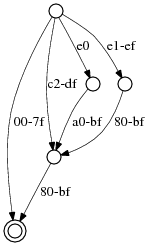
The RE2 compiler has one interesting twist, which I learned from Thompson's grep. It compiles UTF-8 character classes down to an automaton that reads the input one byte at a time. In other words, the UTF-8 decoding is built into the automaton. For example, to match any Unicode code point from 0000 to FFFF (hexadecimal), the automaton accepts any of the following byte sequences:
[00-7F] // code points 0000-007F [C2-DF][80-BF] // code points 0080-07FF [E0][A0-BF][80-BF] // code points 0800-0FFF [E1-EF][80-BF][80-BF] // code points 1000-FFFF
The compiled form is not just the alternation of
those sequences: common suffixes like the [80-BF]
can be factored out. The actual compiled form for this example is:

The example above has the advantage of being fairly regular. Here is the full Unicode range, 000000-10FFFF:
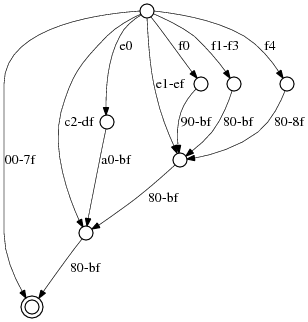
Larger, but still regular.
The real irregularities come from character classes that have
evolved over the course of Unicode's history.
For example, here is \p{Sc}, the currency symbol code points:

The currency symbols are about as complex as will fit in this article,
but other classes are much more complex; for example, look at \p{Greek} (the Greek script) or at \p{Lu} (the uppercase letters).
The result of compilation is an instruction graph like in the last two articles. The representation is closer to the graph in the first but when printed looks like the VM programs in the second.
Compiling out the UTF-8 makes the compiler a little more complicated but makes the matching engines much faster: they can process one byte at a time in tight loops. Also, there turn out to be many matchers; having just one copy of the UTF-8 processing helps keep the code correct.
Everything described until now happens in RE2's constructor.
After the object is constructed, it can be used in a sequence of match operations.
From the user's point of view, there are just two match functions:
RE2::PartialMatch, which finds the first match in the input text,
and RE2::FullMatch, which requires the match to cover the entire input.
From RE2's point of view, though, there are many different questions that
can be asked using them, and the implementation adapts to the question.
RE2 distinguishes four basic regular expression matching problems:
RE2::FullMatch(s, "re") RE2::PartialMatch(s, "^re$")
RE2::PartialMatch(s, "re")
RE2::PartialMatch(s, "(re)", &match)
RE2::PartialMatch(s, "(r+)(e+)", &m1, &m2)
Clearly each is a special case of the next. From the user's point of view, it makes sense to provide just the fourth, but the implementation distinguishes them because it can implement the earlier questions much more efficiently than the later ones.
RE2::FullMatch(s, "re") RE2::PartialMatch(s, "^re$")
This is the question we considered in the first article. In that article we saw that a simple DFA, built on the fly, outperformed all but the other DFA implementations. RE2 uses a DFA for this question too, but the DFA is more memory efficient and more thread-friendly. It employs two important refinements.
Be able to flush the DFA cache. A carefully chosen regular expression and input text might cause the DFA to create a new state for every byte of the input. On large inputs, those states pile up fast. The RE2 DFA treats its states as a cache; if the cache fills, the DFA frees them all and starts over. This lets the DFA operate in a fixed amount of memory despite considering an arbitrary number of states during the course of the match.
Don't store state in the compiled program.
The DFA in the first article used a simple
sequence number field in the compiled program to keep track
of whether a state appeared on a particular list
(s->lastlist and listid).
That tracking made it possible to do list insertion with
duplicate elimination in constant time.
In a multithreaded program, it would be convenient to share
a single RE2 object among multiple threads, which rules out
the sequence number technique.
But we definitely want list insertion with duplicate
elimination in constant time.
Luckily, there is a data structure designed exactly
for this situation: sparse sets.
RE2 implements these in the SparseArray template.
(See “Using Uninitialized Memory for Fun and Profit” for an overview of the idea.)
RE2::PartialMatch(s, "re")
The last question asked whether the regexp matched
the entire string; this one asks whether it matches
anywhere in the string.
We could reduce this question to the last one by
rewriting re into .*re.*,
but we can do better by rewriting it to .*re
and handling the trailing part separately.
Look for a literal first byte.
The DFA or the compiled program form can be analyzed to
determine whether every possible match starts with the same first byte,
like when searching for (research|random).
In this case, when the DFA is looking to start a new match,
it can avoid the general DFA loop and look for the
first byte using memchr,
which is often implemented using special hardware instructions.
Bail out early.
If the question being asked is whether there is a partial match
(e.g., is there a match for ab+ in ccccabbbbddd?),
the DFA can stop early,
once it finds ab. By changing the DFA loop
to check for a match after every byte, it can stop as soon as
there is any match, even if it's not the longest one.
Remember that the caller only cares whether there is a match,
not what it is, so it's okay for the DFA not to look for the longest one.
This sounds like a slightly different DFA than the
one used for the last question, and it is. The DFA code is
written as a single generalized loop that looks at flags controlling
its behavior, like whether there is a literal first
byte to look for or whether to stop as early as possible.
In 2008, when I wrote the DFA code, it was too slow to
check the flags in the inner loop. Instead, the
InlinedSearchLoop
function takes three boolean flags and then is
specialized by calling it from eight different functions
using all the combinations.
When a call must be made, it is to one of the eight
specialized functions rather than the original.
In 2008, this trick created eight different copies
of the search loop, each with a tight inner loop
optimized for its particular case.
I noticed recently that the latest version of g++ refuses
to inline InlinedSearchLoop because it is such
a large function, so there are no longer eight different
copies in the program. It would be possible to reintroduce
the eight copies by making InlinedSearchLoop
a templated function, but it appears not to matter anymore:
I tried that and the specialized code wasn't any faster.
RE2::PartialMatch(s, "(re)", &match)
The caller grows more demanding. Now it wants to know where the match is but still doesn't care about submatch boundaries. We could fall back to the direct NFA simulation, but that carries with it a significant speed penalty compared to the NFA. Instead, with a bit more effort we can squeeze this information out of the DFA.
Find the exact endpoint. Standard presentations of a DFA treat each state as representing an unordered set of NFA states. If instead we treat the DFA state as a partially ordered set of NFA states, we can track which possibilities take priority over others, so that the DFA can identify the exact place where the match stops.
In POSIX rules, states corresponding to matches beginning
earlier in the input take priority over states corresponding
to a later start.
For example, instead of the DFA state representing five NFA states
{1,2,3,4,5} it might represent {1,4}{2,3,5}:
a match arising from states 1 or 4 is
preferred over a match from state 2, 3, or 5.
That takes care of the “leftmost” part of “leftmost longest.”
To implement the “longest” requirement, each time
a match is found in a particular state, the DFA records it and continues
executing only those states that are of equal or higher priority.
Once the DFA runs out of states, the last recorded match position is the end
of the leftmost longest match.
In Perl-style rules, the “leftmost” semantics
are handled the same, but Perl doesn't take the longest of
the leftmost matches. Instead, the state lists are completely ordered: no two
states have equal priority. In an alternation a|b
the states exploring a have higher priortiy than
the states exploring b.
A repetition x* is like a looping alternation that
keeps deciding between looking for another x and
matching the rest of the expression.
Each alternation gives higher priority to looking for another x.
Pictorally, both are Split nodes as in the first article:
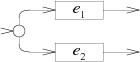
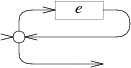
The split gives higher priority to the path leaving out the top. A non-greedy repetition is just a greedy repetition with the priorities reversed.
To find the end of a Perl match, each time a match is found in a particular state, the DFA records it but continues executing only those states of higher priority. Once it runs out of states, the last position it recorded is necessarily the end of the highest priority match.
That's great: now we know where the match ends. But the caller wants to know where the match starts too. How do we do that?
Run the DFA backward to find the start.
When studying regular expressions in a theory of computation
class, a standard exercise is to prove that if
you take a regular expression and reverse all the concatenations
(e.g., [Gg]oo+gle becomes elgo+o[Gg])
then you end up with a regular expression that matches
the reversal of any string that the original matched.
In such classes, not many of the exercises involving
regular expressions and automata have practical value,
but this one does!
DFAs only report where a match ends, but if we run the DFA
backward over the text, what the DFA sees as the end
of the match will actually be the beginning.
Because we're reversing the input, we have to reverse
the regular expression too, by reversing all the concatenations
during compilation.
After compiling a reversed regular expression, we run the DFA backward from the end point found by the forward scan, treating all states as equivalent priority and looking for the longest possible end point. That's the leftmost point in the string where a match could have begun, and since we were careful in the previous step to choose the end of a leftmost match, it's the beginning.
RE2::PartialMatch(s, "(r+)(e+)", &m1, &m2)
This is the hardest question the caller could ask.
Run the DFA to answer the first two parts. The DFA is fast, but it can only answer the first two parts. A direct NFA simulation is necessary to answer the third part. Still, the DFA is fast enough that it makes sense to invoke it for the first two. Using the DFA to find the overall match cuts down the amount of text the NFA must process, which helps when searching large texts for small targets, and it also avoids the NFA completely when the answer to the first question is “no,” a very common case.
Once the DFA finds the match location, it is time to invoke the NFA to find submatch boundaries. The NFA is asymptotically efficient (linear in the size of the regular expression and linear in the size of the input text), but since it must copy around submatch boundary sets, it can be slower in common cases than a backtracker like PCRE. In exchange for guaranteed worst case performance, the average case suffers a little. (For more, see “Regular Expression Matching: the Virtual Machine Approach.”)
A few important common cases don't need the full NFA machinery to guarantee efficient execution. They can be handled with custom code before falling back to the NFA.
Use a one-pass NFA if possible. The NFA spends its time keeping track of multiple submatch boundary sets (in particular, making copies of them), but it is possible to identify a large class of regular expressions for which the NFA never needs to keep more than one set of boundary positions, no matter what the input.
Let's define a “one-pass regular expression”
to be a regular expression with the property that
at each input byte during an anchored match, there is only
one alternative that makes sense for a given input byte.
For example, x*yx* is one-pass: you read
x's until a y, then you read the y, then you keep reading x's.
At no point do you have to guess what to do or back up
and try a different guess.
On the other hand, x*x is not one-pass: when you're
looking at an input x, it's not clear whether you should
use it to extend the x* or as the final x.
More examples: ([^x]*)x(.*) is one-pass;
(.*)x(.*) is not. (\d+)-(\d+) is one-pass; (\d+).(\d+) is not.
A simple intuition for identifying one-pass regular expressions
is that it's always immediately obvious when a repetition ends.
It must also be immediately obvious which branch of an | to take:
x(y|z) is one-pass, but (xy|xz) is not.
Because there's only one possible next choice, the one-pass NFA implementation never needs to make a copy of the submatch boundary set. The one-pass engine executes in two halves. During compilation, the one-pass code analyzes the compiled form of the program to determine whether it is one-pass. If so, the engine computes a data structure recording what to do at each possible state and input byte. Then at execution the one-pass engine can fly through the string, finding the match (or not) in, well, one pass.
Use a bit-state backtracker if possible. Backtrackers like PCRE avoid the copying of the submatch sets: they have a single set and overwrite and restore it during the recursion. For correctness, such an approach must be willing to revisit the same part of a string multiple times, at least one time per NFA state. That would still only be a linear time scan, though: the exponential time part of PCRE comes in revisiting the same part of a string many times per NFA state, because the algorithm does not remember that it has been down a particular path before.
The bit-state backtracker takes the standard backtracking algorithm, implemented with a manual stack, and adds a bitmap tracking which (state, string position) pairs have already been visited. For small regular expressions matched against small strings, allocating and clearing the bitmap is significantly cheaper than the copying of the NFA states. RE2 uses the bit state backtracker when the bitmap is at most 32 kilobytes.
If all else fails, use the standard NFA.
RE2 disallows PCRE features that cannot be implemented
efficiently using automata. (The most notable such feature is backreferences.)
In return for giving up these difficult to implement (and often incorrectly used)
features, RE2 can provably analyze the regular expressions or the
automata.
We've already seen examples of analysis for use in RE2 itself,
in the DFA's use of memchr and in the analysis of
whether a regular expression is one-pass.
RE2 can also provide analyses that let higher-level applications
speed searches.
Match ranges.
Bigtable stores records
in order stored by row name, making it efficient to scan all rows with names
in a given range. Bigtable also allows clients to specify a regular expression filter:
the scan skips rows with names that are not an exact match for the regular expression.
It is convenient for some clients to use just the regular expression filter
and not worry about setting the row range. Those clients can improve the
efficiency of such a scan by asking RE2 to compute the
range of strings that could possibly match the regular expression
and then limiting the scan to just that range.
For example, for (hello|world)+, RE2::PossibleMatchRange
can determine that all possible matches are in the range [hello, worldworle].
It works by exploring the DFA graph from the start state,
looking for a path with the smallest possible byte values
and a path with the largest possible byte values.
The e at the end of worldworle is a not a typo:
worldworldworld < worldworle but not worldworld:
PossibleMatchRange must often truncate the strings used
to specify the range, and when it does, it must round the upper bound up.
Required substrings.
Suppose you have an efficient way to check which of a list of strings
appear as substrings in a large text (for example, maybe you implemented
the Aho-Corasick algorithm),
but now your users want to be able to do regular expression searches efficiently too.
Regular expressions often have large literal strings in them; if those could be
identified, they could be fed into the string searcher, and then the results of
the string searcher could be used to filter the set of regular expression searches
that are necessary.
The FilteredRE2 class
implements this analysis. Given a list of regular expressions, it walks the regular
expressions to compute a boolean expression involving literal strings
and then returns the list of strings.
For example, FilteredRE2 converts
(hello|hi)world[a-z]+foo into the boolean expression
“(helloworld OR hiworld) AND foo”
and returns those three strings.
Given multiple regular expressions, FilteredRE2 converts
each into a boolean expression and returns all the strings involved.
Then, after being told which of the strings are present,
FilteredRE2 can evaluate each expression
to identify the set of regular expressions that could possibly be present.
This filtering can reduce the number of actual regular expression searches significantly.
The feasibility of these analyses depends crucially on the simplicity
of their input. The first uses the DFA form, while the second uses the parsed
regular expression (Regexp*).
These kind of analyses would be more complicated
(maybe even impossible)
if RE2 allowed non-regular features in its regular expressions.
RE2 treats regular expressions as describing Unicode sequences
and can search text encoded in UTF-8 or Latin-1.
Like PCRE and other regular expression implementations,
named groups like [[:digit:]] and \d
contain only ASCII, but Unicode property groups like \p{Nd}
contain full Unicode.
The challenge for RE2 is to implement the large
Unicode character set efficiently and compactly.
We saw above that a character class is represented
as a balanced binary tree, but it is also important to
keep the library footprint small, which means
tight encoding of the necessary Unicode tables.
For internationalized character classes, RE2 implements
the Unicode 5.2 General Category property
(e.g., \pN or \p{Lu})
as well as the Unicode Script property
(e.g., \p{Greek}).
These should be used whenever matches are not intended
to be limited to ASCII characters
(e.g., \pN or \p{Nd} instead of [[:digit:]] or \d).
RE2 does not implement the other Unicode properties
(see Unicode Technical Standard #18: Unicode Regular Expressions).
The Unicode group table maps a group name to an array of
code ranges defining the group.
The Unicode 5.2 tables require 4,258 code ranges.
Since Unicode has over 65,536 code points, each range
would normally require two 32-bit numbers (start and end),
or 34 kilobytes total.
However, since the vast majority of ranges involve only
code points less than 65,536, it makes sense to split each
group into a set of 16-bit ranges and a set of 32-bit ranges,
cutting the table footprint to 18 kilobytes.
RE2 implements case-insensitive matches (enabled by (?i)) according to
the Unicode 5.2 specification:
it folds
A with a, Á with á,
and even K with K (Kelvin) and S with ſ (long s).
There are 2,061 case-specific characters.
RE2's table map each Unicode code point to the next
largest point that should be treated as the same.
For example, the table maps
B to b and
b to B.
Most of these loops involve just two characters, but there
are a few longer ones: for example,
the table maps
K to k, k to K (Kelvin symbol),
and K back to K.
That table is very repetitive: A maps to a, B maps to b, and so on.
Instead of listing every character, we can list ranges and deltas:
A through Z map to the value plus 32,
a through j map to the value minus 32,
k maps to K (Kelvin symbol again), and so on.
There is a special case for ranges with runs of upper/lower pairs and
lower/upper pairs.
This encoding cuts the table from 2,061 entries taking 16 kilobytes to
279 entries taking 3 kilobytes.
RE2 does not implement named characters like in Python's u"\N{LATIN SMALL LETTER X}" as an alias for "x".
Even ignoring the obvious user interface issues, the necessary table would be around 150 kilobytes.
How do we know that the RE2 code is correct? Testing a regular expression implementation is a complex undertaking, especially when the implementation has as many different code paths as RE2. Other libraries, like Boost, PCRE, and Perl, have built up large, manually maintained test suites over time. RE2 has a small number of hand-written tests to check basic functionality, but it quickly became clear that hand-written tests alone would require too much effort to create and maintain if they were to cover RE2 well. Instead, the bulk of the testing is done by generating and checking test cases mechanically.
Given a list of small regular expressions and operators,
the RegexpGenerator class generates all possible expressions using those
operators up to a given size. Then the StringGenerator generates all possible
strings over a given alphabet up to a given size.
Then, for every regular expression and every input string, the RE2 tests check that
the output of the four different regular expression engines
agree with each other, and with a trivial backtracking
implementation written only for testing,
and (usually) with PCRE itself.
RE2 does not match PCRE on all cases, so the tester includes
an analysis to check for cases
on which RE2 and PCRE disagree, as listed in the Caveats section below.
Except when the regular expression involves these boundary cases,
the tester requires RE2 and PCRE to agree
on the outcome of the match.
The exhaustive tests must limit themselves to small regular expressions
and small input strings, but most bugs can be exposed by small test cases.
Enumerating all small test cases catches almost all the mistakes that get past the
few hand-written tests.
Even so, RE2 also includes a randomized tester, variants of the
RegexpGenerator and StringGenerator
that generate larger random instances.
It's rare for random testing to catch something
that the smaller exhaustive testing missed,
but it is still a good reassurance that large expressions and texts
continue to work correctly.
RE2 is competitive with PCRE on small searches and faster on large ones. The performance for small searches is reported in microseconds, since the search time is mostly independent of the actual text size (around 10 bytes in these examples). The performance on large searches is reported in MB/s, since the search time is typically linear in the actual text size.
The benchmarks reported are run by re2/testing/regexp_benchmark.cc. The directory re2/benchlog holds accumulated results.
(All tests are run with PCRE 8.01, the latest version at time of writing.)
Compilation. RE2 compiles regexps at about 3-4x slower than PCRE:
|
||||||||||||||||||
| Time to compile a simple regular expression. | ||||||||||||||||||
The difference is about 5-10 microseconds per regexp. These timings include time spent freeing the regexp after parsing and compilation. We expect that the common case is that regexps are cached across matches when speed is critical, making compile time not too important.
The compiled form of an RE2 is bigger than that of a PCRE object, a few kilobytes vs a few hundred bytes for a typical small regular expression. RE2 does more analysis of the regexp during compilation and stores a richer form than PCRE. RE2 saves state (the partially-built DFA) across calls too: after running a few matches a simple RE2 might be using 10kB, but more matches do not typically increase the footprint. RE2 limits total space usage to a user-specified maximum (default 1MB).
Full match, no submatch info.
We saw above that some searches are harder than others
and that RE2 uses different implementations for different kinds of searches.
This benchmark searches for .*$
in a randomly-generated input text of the given size.
It gives a sense of the flat out search speed.
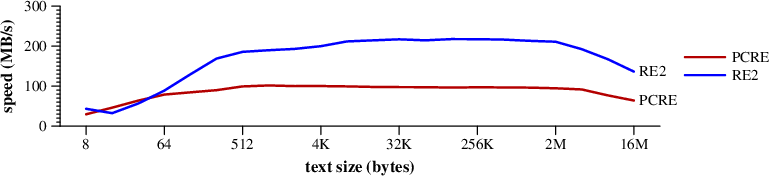
|
Speed of searching for .*$ in random text. (Mac Pro) |
RE2 uses a DFA to run the search.
Full match, one-pass regular expression, submatch info, tiny strings.
This benchmark searches for ([0-9]+)-([0-9]+)-([0-9]+)
in the string 650-253-0001, asking for the location of the three submatches:
|
||||||||||||||||||
Time to match ([0-9]+)-([0-9]+)-([0-9]+) in 650-253-0001. | ||||||||||||||||||
RE2 uses the OnePass matching engine to run the search, avoiding the overhead of the full NFA.
Full match, ambiguous regular expression, submatch info, tiny strings.
If the regexp is ambiguous, RE2 cannot use the OnePass engine,
but if the regexp and string are both small, RE2 can use the BitState engine.
This benchmark searches for [0-9]+.(.*) in 650-253-0001:
|
||||||||||||||||||
Time to match [0-9]+.(.*) in 650-253-0001. | ||||||||||||||||||
Here, RE2 is noticeably slower than PCRE, because the regexp is not
unambiguous: it is never clear whether an additional digit should
be added to the [0-9]+ or used to match the ‘.’.
PCRE is optimized for matches; when presented with strings
that don't match, its run-time can grow exponentially in the
worst case, and is noticeably slower even in common cases.
In contrast, RE2 plods along at linear speed regardless of
whether the text matches.
The particular speed depends on the size of the text and regexp.
In small cases like this one, RE2 uses BitState; in larger cases,
it must fall back to NFA.
Partial match, no actual match. Looking for a partial (unanchored) match requires that the matching engine consider matches starting at every byte in the string. PCRE implements this as a loop that tries starting at each byte in the string, while the RE2 implementations can run all of those in parallel. The RE2 implementations analyze the regexp more thoroughly than PCRE does, leading to potential speedups.
This benchmark searches for ABCDEFGHIJKLMNOPQRSTUVWXYZ$
in randomly generated text.
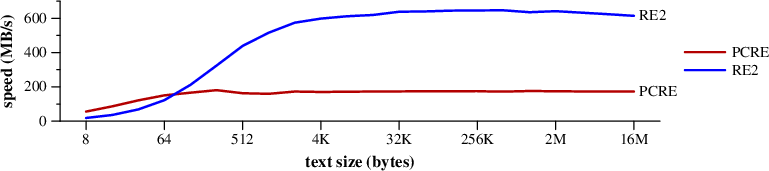
|
Speed of searching for ABCDEFGHIJKLMNOPQRSTUVWXYZ$ in random text. (Mac Pro) |
The RE2 DFA spends most of its time
in memchr looking for the leading A.
PCRE notices the leading A too, though it
seems not to take as much advantage.
I suspect that PCRE does not continue to use memchr
after finding the first A.
The next benchmark is a little harder, since there is no
leading character to memchr for.
It looks for [XYZ]ABCDEFGHIJKLMNOPQRSTUVWXYZ$.
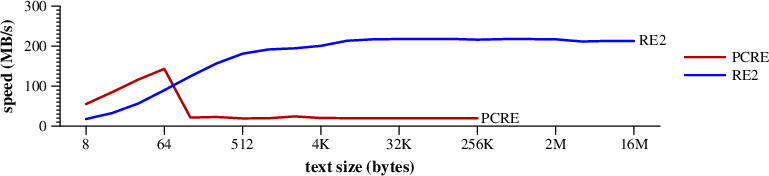
|
Speed of searching for [XYZ]ABCDEFGHIJKLMNOPQRSTUVWXYZ$ in random text. (Mac Pro) |
PCRE falls back on much slower processing to handle it, while RE2's DFA runs its fast byte-at-a-time loop.
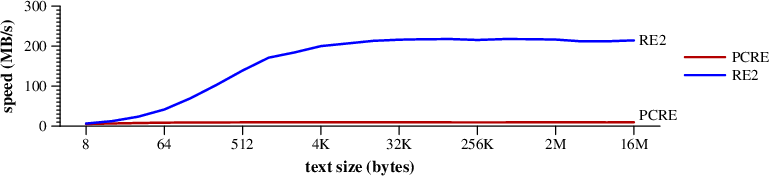
The next benchmark is quite difficult for PCRE.
It looks for [ -~]*ABCDEFGHIJKLMNOPQRSTUVWXYZ$.
The text has no match for that expression, but PCRE scans the
entire string at each position matching [ -~]*
before realizing there is no match there.
This ends up taking O(text2) time to match.
RE2's DFA makes a single linear pass.

|
Speed of searching for [ -~]*ABCDEFGHIJKLMNOPQRSTUVWXYZ$ in random text. (Mac Pro) |
Notice that PCRE sputters out at texts 4K in length.
Search and parse.
Another typical use of RE is to find and parse a particular string
in a text. This benchmark generates a random text with
(650) 253-0001 at the end and then does an
unanchored search for (\d{3}-|\(\d{3}\)\s+)(\d{3}-\d{4}),
extracting the area code separately from the 7-digit phone number.
|
Speed of searching for and matching (\d{3}-|\(\d{3}\\)\s+)(\d{3}-\d{4})
in random text ending wtih (650) 253-0001. (Mac Pro) |
RE2's faster DFA searching is responsible for the improved speed.
Summary. RE2 requires about 10 KB per regexp, in contrast to PCRE's half a KB or so. In exchange for the extra space, RE2 guarantees linear-time performance, although the linear-time constant varies by situation.
RE2 runs at about the same speed as PCRE for queries that ask whether
a string matches but do not ask for submatch information
(e.g., RE2::FullMatch or RE2::PartialMatch
with no additional arguments).
When using regexps to parse text, RE2 runs at about the same speed as PCRE for unambiguous regexps. It runs at about half the speed for ambiguous regexps with small matches, and considerably slower for ambiguous regexps with large matches. The data sizes involved in these cases are usually small enough that the run-time difference is not a bottleneck. (For example, any performance loss parsing a file name vanishes in comparison to the time required to open the file.)
RE2 excels at searches over large amounts of text. It can locate matches much faster than PCRE, especially if the search requires PCRE to backtrack.
These benchmarks compare against PCRE because it is the most direct comparison: C/C++ against C/C++, with an almost identical interface. It's important to emphasize that the benchmarks are interesting because they primarily compare algorithms, not performance tuning. PCRE's choice of algorithm, at least in the general case, is forced by the attempt to be completely compatible with Perl and friends.
RE2 explicitly does not attempt to handle every extension that
Perl has introduced.
The Perl extensions it supports are:
non-greedy repetition; character classes like \d; and
empty assertions like \A, \b, \B, and \z.
RE2 does not support arbitrary lookahead or lookbehind assertions,
nor does it support backreferences.
It supports counted repetition, but it is implemented by
actual repetition (\d{3} becomes \d\d\d),
so large repetition counts are unwise.
RE2 supports Python-style named captures (?P<name>expr),
but not the alternate syntaxes (?<name>expr) and (?'name'expr)
used by .NET and Perl.
RE2 does not always match PCRE's behavior. There are a few known instances where RE2 intentionally differs:
(a*)+, then PCRE will treat the reptition
sequence as ending with an empty string, while RE2 does not.
Specifically, when matching (a*)+ against aaa,
PCRE runs the + twice, once to match aaa
and a second time to match the empty string. RE2 runs the +
only once, to match aaa. Because parens capture the
rightmost text they matched, for PCRE $1
will be an empty string while for RE2 $1 will be aaa.
The PCRE behavior could be kludged into RE2 if needed.
\v.
In Perl it matches just the vertical tab character (VT, 0x0B),
while in PCRE it matches both the vertical tab and newline.
RE2 chooses to side with Perl.
$ to match either before or after
that final newline.
RE2 requires that it match after, at the very end of the text.
^, which normally
matches following a newline, to match at the very end of the text.
RE2 does.
[[:^xxx:]] to match only ASCII code points,
so that [[:^alpha:]] matches ASCII characters that are not in [[:alpha:]],
while [^[:alpha:]] matches any Unicode character that is not in [[:alpha:]].
RE2 corrects this inconsistency:
[[:^alpha:]] and [^[:alpha:]] both mean any Unicode
character that is not in [[:alpha:]].
There are a handful of obscure features of Perl and PCRE that RE2 chooses not to implement. These are:
\q should mean something special
and \# should match a literal #.
Perl and PCRE accept escaped letters as literals
if the letter does not (yet) have a meaning.
Thus in Perl, \q matches a literal q,
at least until a different meaning is introduced.
RE2 rejects unknown escaped letters rather than
silently treating them as literals.
This also helps diagnose uses of sequences that
RE2 does not support, like \cx (see below).
\cx as the Control-X character.
Embed a literal control character using C++ string syntax
or an octal or hexadecimal escape.
\b means backspace.
In Perl, it means word boundary,
except inside a character class, when it means backspace ([\b]).
RE2 attempts to avoid confusion by never recognizing
\b as backspace.
RE2 rejects \b in POSIX mode,
recognizes it as word boundary in Perl mode,
and always rejects it in character classes.
To match a backspace, embed a literal backspace character or write \010.
(?>...) and ++.
These are used mainly as a performance band-aid for backtracking.
RE2 provides a more complete solution.
\C, \G or \X.
(?(...)...),
comments (?#...), pattern references (?R) (?1)
(?P>foo),
or C callouts (?C...).
By default, RE2 enforces a maximum of 1MB (per RE2 object)
for the two Progs and their DFAs.
This is enough for most expressions, but very large expressions
or patterns with large counted repetitions may exceed
these limits.
Running out of memory during compilation
causes re.ok() to return false,
with an explanation in re.error().
RE2 cannot run out of memory during a text search:
it will discard the cached DFA and start a new DFA
using the reclaimed memory.
If it must discard the DFA too often, it will fall back
on an NFA search.
RE2 demonstrates that it is possible to use automata theory to implement almost all the features of a modern backtracking regular expression library like PCRE. Because it is rooted in the theoretical foundation of automata, RE2 provides stronger guarantees on execution time than and enables high-level analyses that would be difficult or impossible with ad hoc implementations. Finally, RE2 is open source. Have fun!
RE2's implementation and my understanding of regular expressions
have both benefited greatly from discussions with Rob Pike and
Ken Thompson over the last few years.
Sanjay Ghemawat designed and implemented the C++ interface to PCRE,
which RE2's C++ interface mimics and is derived from.
Srinivasan Venkatachary wrote the FilteredRE2 code.
Philip Hazel's PCRE is an astonishing
piece of code. Trying to match most of PCRE's regular expression features
has pushed RE2 much farther than it would otherwise have gone,
and PCRE has served as an excellent implementation against which to test.
Thanks to all.
The next article in this series is “Regular Expression Matching with a Trigram Index,” a behind-the-scenes look at how Google Code Search worked.
Copyright © 2010 Russ Cox. All Rights Reserved.
https://swtch.com/~rsc/regexp/